Probabilité EuroMillion Calcul - Loi hypergéométrique & simulateur avec R

Reading time ~ 10 minutes ->
1. Calculateur de probabilité euromillions : Introduction
Les jeux de hasard et des super loteries font rêver énormément de joueurs dans le monde. Il faut dire que les sommes annoncées pour les rangs de gains et plus particulièrement pour le rang 1 sont élevées. Prenez l’EuroMillions, le gain maximum possible est de 190,000,000 €. Ce qui fait le jeu de hasard avec le plus gros gain en Europe.
Nous savons pourtant qu’il s’agit avant tout de probabilités, qu’il existe des millions de combinaisons et que les chances de remporter le gros lot sont assez minces. Prenez le rang 1, la chance de gagner le jackpot équivaut à 1 chance sur 139,838,160.
Mais qu’est-ce la probabilité ? Simplement exprimé, c’est un indicateur mesurant la chance ou le risque qu’un événement se produise. Mathématiquement, c’est un nombre compris entre 0 et 1. Plus la valeur est proche de 1, plus la chance que l’événement se produise est grande. C’est aussi le rapport du nombre de cas favorable au nombre de cas possible.
Pour gagner au rang 1, il faut trouver la bonne combinaison, à savoir les 5 numéros et les 2 étoiles. Si on s’intéresse à la probabilité qu’un numéro donné soit tiré (laissons les étoiles de côté) nous devons calculer le nombre de grilles possibles ou ce numéro apparaît. Avant d’aller plus loin, intéressons-nous à l’analyse combinatoire.
2. Analyse combinatoire

L’analyse combinatoire fournit entre autres des formules pour calculer le nombre d’arrangements possibles de n objets pris k à la fois ou le nombre de combinaisons de n objets pris k à la fois ou le nombre de permutations des n éléments d’un ensemble. Allons-y !
2.1. Permutations sans répétition
La permutation c’est lorsque nous cherchons le nombre de réarrangement possible d’objets et cela de manière différente. Ici l’ordre à son importance et donc nous comptabilisons toutes les façons d’ordonner les objets observés. Pour le calcul de ce nombre, nous utilisons la factorielle. La factorielle d’un nombre entier s’écrit avec un point d’exclamation n!. Cette notion a été introduite par Christian Kramp en 1808. La factorielle va être utilisée dans les différentes formules de ce post.
Par ex. pour calculer le nombre de mots possibles avec 10 lettres sans lettre répétée, nous calculons la factorielle de 10, soit 10! mots possibles.
permutation <- function(n) {factorial(n)}permutation(10)## [1] 3628800Cela nous donne 3,628,800 façons d’écrire un mot avec 10 lettres données.
2.2. Arrangement
L’arrangement est le tirage d’une quantité d’objets avec ordre dans un ensemble d’objets. Comme le tiercé dans l’ordre par ex. En réalité, une permutation est un arrangement avec le tirage de tous les objets. Pour l’exemple précédent cela consiste à écrire nos mots avec toutes les lettres données. Des mots de 10 lettres donc.
La formule :
arrangement <- function(n, k) {
factorial(n) / (factorial(n - k))
}Ex.
arrangement(10, 10)## [1] 3628800Si nous composons des mots de 3 lettres uniquement, nous avons 720 combinaisons possibles avec les 10 lettres données et différentes.
arrangement(10, 3)## [1] 7202.3. Combinaisons
La combinaison est le tirage d’une quantité d’objets sans ordre dans un ensemble d’objets, par ex. {a, b} et {b, a} est compté qu’une seule fois. C’est ce qui nous intéresse pour l’EuroMillions car l’ordre du tirage importe peu. Un tirage de 5 boules dans un ensemble de 50. C’est le jackpot peu importe l’ordre.
Voici la formule :
combinaison <- function(n, k) {
factorial(n) / (factorial(k) * (factorial(n - k)))
}combinaison(10, 3)## [1] 120Le nombre de combinaison est 6x moins que l’arrangement, car on supprime toutes les combinaisons obtenues avec 3 lettres identiques. Combien-avons nous de combinaisons permutations pour 3 lettres ? Nous en avons 3! donc 6 (3x2).
3. Jouons à l’EuroMillions

3.1. Trouver les 5 numéros et les 2 étoiles
Souvenez-vous, une grille est composée de 5 numéros et de 2 étoiles. Intéressons-nous à la première partie et le nombre de combinaisons possibles (l’ordre n’a pas d’importantce) d’une grille de 5 numéros parmi les 50 boules dansantes devant nous.
combinaison(50, 5)## [1] 2118760Nous avons donc 2,118,760 grilles possibles. Choisissons le numéro 50 par ex. Quel est le nombre de grille où le numéro 50 apparait ? Pour faciliter le calcul, enlevons le numéro 50 de notre urne, ce qui laisse 49 boules. Combien existe-t-il de grilles possibles ?
combinaison(49, 4)## [1] 211876Il existe 211,876 grilles. N’oublions pas que l’ordre n’a pas d’importance. Rajoutons le 50 à ces grilles cela nous fait toujours 211,876 combinaisons sur les 2,118,760. Donc une probabilité de 211,876 / 2,118,760. Ce qui équivaut à :
211876 / 2118760## [1] 0.11 chance sur 10 que le numéro 50 sorte à chaque tirage. Il en va de même pour tous les numéros.
3.2. La loi hypergéométrique
La loi hypergéométrique permet de calculer la probabilité d’un tirage dans un tirage. Nous pourrions calculer la probabilité d’avoir 1, 2, 3, 4 ou 5 bons numéros dans un tirage de 5 parmi les 50 numéros. Bien souvent la loi hypergéométrique est illustrée avec des boules blanches et noires dans une urne. Nous allons ici considérer que les boules gagnantes sont nos boules blanches et les autres les boules noires. Ce qui nous donne :
Dans l’urne il y a 50 boules x = 50, dont 5 gagnantes m = 5,
Nous tirons 5 boules n = 5, et nous souhaitons avoir 1 boule gagnante parmi les 5 boules tirées k = 1.
La formule est la suivante :
\(\Large P(k) = \frac{\binom{m}{k}\binom{x-m}{n-k}}{\binom{x}{n}}\)
La fonction :
hyper <- function(x, m, n, k) {
combinaison(m, k) * combinaison(x - m, n - k) / combinaison(x, n)
}Testons et examinons la probabilité d’avoir un numéro gagnant dans 1 grille :
hyper(x = 50, m = 1, n = 5, k = 1)## [1] 0.1Nous obtenons bien 0.1. Ceci est identique au calcul précédant où nous avons divisés le nombre de grille à 49 numéros avec le nombre de grilles avec 50 boules. Remplaçons nos valeurs x, m, n et k dans la formule :
\(\Large P(k) = \frac{\binom{1}{1}\binom{50-1}{5-1}}{\binom{50}{5}}\)
Nous retrouvons notre résultat 211876 / 2118760.
3.3. Vérification
J’aime faire une simulation pour corroborer ce résultat. L’approche est toute simple, elle consiste à simuler des grilles de 5 numéros. Je map la fonction sample sur un vecteur (1:1000). Ce qui me donne une liste de 100,000 grilles de 5 boules.
grid <- map(1:100000, ~ sample(50, 5))
head(grid, 3)## [[1]]
## [1] 34 3 21 43 36
##
## [[2]]
## [1] 18 43 7 4 50
##
## [[3]]
## [1] 8 48 14 46 23Générons le numéro gagnant :
winner <- sample(50, 1)
winner## [1] 12Et comparons chaque grille avec le numéro gagnant grâce à la fonction %in%.
Le résultat de la comparaison est une valeur logique TRUE ou FALSE.
res <- map(grid, ~ winner %in% .)
head(res, 3)## [[1]]
## [1] FALSE
##
## [[2]]
## [1] FALSE
##
## [[3]]
## [1] FALSEPour rappel, nous cherchons la probabilité d’avoir 1 bon numéro dans une grille simple. Nous simulons donc un nombre important de grilles simples (en réalité nous devrions tendre vers l’infini pour s’approcher du résulat de notre formule hypergéométrique). Nous comparons, puis calculons la valeur de chaque grille. Ce qui nous intéresse ce sont les grilles avec la valeur égale à 1, c’est à dire dont le résulat de notre comparaison équivaux à 1 TRUE sur les 4, soit un numéro qui apparait dans la combinaison au tirage gagnant.
Pour cela, je transforme les valeurs logiques en numériques puis cacule la somme de chaque grille, compare si la somme équivaux à 1, si oui, j’obtiens un TRUE, si non un FALSE que je transforme à nouveau en numérique (donc de valeur 0 ou 1). L’astuce consiste ensuite à calculer la moyenne pour obtenir le ratio des grilles gagnantes.
map(res, as.numeric) %>%
map(sum) %>%
map(~ . == 1) %>%
as.numeric() %>%
mean() ## [1] 0.09813CQFD, le résultat s’approche du résultat de notre fonction hypergéométrique, à savoir 0.1.
Ou simplement dit, 1 grille sur 10 contient le numéro gagnant.
Calculons d’autres probabilités de gain de l’euro million. Petit détail qui a son importance, je me mets dans les conditions de l’euro million soit 5 numéros et 2 étoiles donc en multipliant les 2 probabilités. Je me suis intérrogé sur les raisons de le faire même lorsque la condition des étoiles vaut 0, k = 0. En réalité, si on compare les 2 résultats, on peut s’apercevoir que la probabilité n’est pas la même. Mais Pourquoi, puisque nous cherchons la probabilité d’obtenir seulement 2 numéros gagnants dans la grille ? Après réflexion, c’est assez logique pusique la probabilité d’avoir 0 étoiles ne vaut pas 0 mais bien 0.68 :
hyper(x = 12, m = 2, n = 2, k = 0)## [1] 0.6818182Si la combinaison gagnante ne comprenait que 5 numéros, notre chance d’obtenir 2 bons numéros serait de 1 chance sur 15. Mais l’ajout des 2 étoiles fait “tomber” la probabilité à 1 chance sur 22 même avec 0 étoile de trouvée. Logique car il y une probabilité d’obtenir 1 étoiles voir 2 donc il faut considérer aussi la probabilité d’en avoir 0. Voyons cela :
Avec les étoiles en plus :
1 / (hyper(x = 50, m = 5, n = 5, k = 2) * hyper(x = 12, m = 2, n = 2, k = 0))## [1] 21.89933Sans les étoile :
1 / hyper(x = 50, m = 5, n = 5, k = 2)## [1] 14.931363.4. Quelques combinaisons et leur probabilité :
2numéros gagnants et0étoile (k = 2 et k = 0) :1 chance sur 22
1 / (hyper(x = 50, m = 5, n = 5, k = 2) * hyper(x = 12, m = 2, n = 2, k = 0))## [1] 21.899332numéros gagnants et1étoile (k = 2 et k = 0) :1 chance sur 49
1 / (hyper(x = 50, m = 5, n = 5, k = 2) * hyper(x = 12, m = 2, n = 2, k = 1))## [1] 49.273494numéros gagnants et2étoiles (k = 2 et k = 0) :1 chance sur 621,502
1 / (hyper(x = 50, m = 5, n = 5, k = 4) * hyper(x = 12, m = 2, n = 2, k = 2))## [1] 621502.95numéros gagnants et0étoile (k = 2 et k = 0) :1 chance sur 3,107,515
1 / (hyper(x = 50, m = 5, n = 5, k = 5) * hyper(x = 12, m = 2, n = 2, k = 0))## [1] 31075155numéros gagnants et2étoiles (k = 2 et k = 0) :1 chance sur 139,838,160
1 / (hyper(x = 50, m = 5, n = 5, k = 5) * hyper(x = 12, m = 2, n = 2, k = 2))## [1] 1398381604. Simulateur

Pour réaliser notre simulateur, nous allons écrire une fonction principale simulant un tirage et une comparaison avec un certain nombre de grilles (l’argument de notre fonction sera le nombre de grilles). Nous ajouterons aussi une table afin d’attribuer un gain à chaque grille.
4.1. Le tirage
Nous utilisons la fonction sample.int pour générer 5 numéros sans répétition (replace = FALSE).
Idem pour les 2 étoiles
draw_n <- sample.int(50, 5, replace = FALSE)
draw_s <- sample.int(12, 2, replace = FALSE)4.2. La grille
Créons d’abord l’argument grid avec la valeur 1 de départ qui définira le nombre de grilles jouées :
grid <- 1Initialisons 2 listes de longueur grid. Ceci nous servira de conteneur pour l’ensemble des grilles générées :
grid_n <- vector("list", grid)
grid_s <- vector("list", grid)Puis une boucle pour générer nos grilles :
for(i in 1:grid) {
grid_n[[i]] <- sample.int(50, 5, replace = FALSE) %>% sort()
grid_s[[i]] <- sample.int(12, 2, replace = FALSE) %>% sort()
}Vérifions :
head(grid_n, 1)## [[1]]
## [1] 14 25 43 45 46head(grid_s, 1)## [[1]]
## [1] 9 124.3. Le résultat
Vient le moment de vérifier si nos grilles comportent la combinaison gagnante. Nous allons comparer chaque numéro de chaque grille avec le tirage. Nous obtiendrons avec la fonction %in% une valeur logique TRUE si les numéros correspondent, FALSE dans le cas contraire. Nous avons appliqué le même principe précédemment avec comme différence le fait que nous calculons la somme de chaque comparatif obtenu via la fonction sum directement. La fonction map exécute notre fonction sur chaque grille de la liste. Si nous obtenons une valeur de 5, cela signifie que les 5 numéros sont gagnants.
result_n <- grid_n %>% map(~ sum(. %in% draw_n))
result_s <- grid_s %>% map(~ sum(. %in% draw_s))4.4. Les gains
Maintenant nous transformons nos 2 listes en une table de 2 colonnes dont chaque rang correspond à une grille.
Nous ajoutons la valeur d’achat de la grille et une colonne supplémentaire avec le gain obtenu. Pour cela nous utilisons la fonction case_when pour attribuer le gain en fonction de la valeur des 2 premières colonnes.
tibble("n" = flatten_int(result_n), "e" = flatten_int(result_s)) %>%
mutate(cost = 2.5) %>%
mutate(gain = case_when(
n == 0 & e == 0 ~ 0,
n == 0 & e == 1 ~ 0,
n == 0 & e == 2 ~ 0,
n == 1 & e == 0 ~ 0,
n == 1 & e == 1 ~ 0,
n == 1 & e == 2 ~ 0,
n == 2 & e == 0 ~ 4,
n == 2 & e == 1 ~ 8,
n == 1 & e == 2 ~ 10,
n == 3 & e == 0 ~ 12,
n == 3 & e == 1 ~ 14,
n == 2 & e == 2 ~ 19,
n == 3 & e == 2 ~ 59,
n == 4 & e == 0 ~ 101,
n == 4 & e == 1 ~ 201,
n == 4 & e == 2 ~ 4143,
n == 5 & e == 0 ~ 51792,
n == 5 & e == 1 ~ 310751,
n == 5 & e == 2 ~ 1700000
)) ## # A tibble: 1 × 4
## n e cost gain
## <int> <int> <dbl> <dbl>
## 1 0 0 2.5 04.5. La fonction
Combinons maintenant l’ensemble dans une fonction. Nous ajoutons juste une synthèse des résultats avec la fonction summarize.
play <- function(grid = 1) {
draw_n <- sample.int(50, 5, replace = FALSE) %>% sort()
draw_s <- sample.int(12, 2, replace = FALSE) %>% sort()
grid_n <- vector("list", grid)
grid_s <- vector("list", grid)
for(i in 1:grid) {
grid_n[[i]] <- sample.int(50, 5, replace = FALSE) %>% sort()
grid_s[[i]] <- sample.int(12, 2, replace = FALSE) %>% sort()
}
result_n <- grid_n %>% map(~ sum(. %in% draw_n))
result_s <- grid_s %>% map(~ sum(. %in% draw_s))
tibble("n" = flatten_int(result_n), "e" = flatten_int(result_s)) %>%
mutate(cost = 2.5) %>%
mutate(gain = case_when(
n == 0 & e == 0 ~ 0,
n == 0 & e == 1 ~ 0,
n == 0 & e == 2 ~ 0,
n == 1 & e == 0 ~ 0,
n == 1 & e == 1 ~ 0,
n == 1 & e == 2 ~ 0,
n == 2 & e == 0 ~ 4,
n == 2 & e == 1 ~ 8,
n == 1 & e == 2 ~ 10,
n == 3 & e == 0 ~ 12,
n == 3 & e == 1 ~ 14,
n == 2 & e == 2 ~ 19,
n == 3 & e == 2 ~ 59,
n == 4 & e == 0 ~ 101,
n == 4 & e == 1 ~ 201,
n == 4 & e == 2 ~ 4143,
n == 5 & e == 0 ~ 51792,
n == 5 & e == 1 ~ 310751,
n == 5 & e == 2 ~ 1700000
)) %>%
summarise(t_cost = sum(cost), t_gain = sum(gain)) %>%
mutate(bank = t_gain - t_cost)
}Testons notre fonction pour 10 grilles :
play(10)## # A tibble: 1 × 3
## t_cost t_gain bank
## <dbl> <dbl> <dbl>
## 1 25 4 -21Et pour 1,000 grilles jouées dans un tirage :
play(1000)## # A tibble: 1 × 3
## t_cost t_gain bank
## <dbl> <dbl> <dbl>
## 1 2500 457 -20434.6. Une autre fonction avec notre fonction
Comparer n grilles à 1 tirage est sympa, mais comment faire si nous souhaitons simuler plusieurs tirage ? La programmation fonctionnelle va nous permettre d’y arriver. Le livre Advanced R (Hadley Wickham) traite très bien ce sujet.
2 arguments : le nombre de tirages et le nombre de grilles par tirage. Le coeur de la fonction c’est l’exécution de notre fonction play sur un vecteur de longueur draw.
multi_play <- function(draw = draw, grid = grid) {
map_dfr(rep(grid, draw), play)
}Résultat pour la participation à 2 tirages avec 2 grilles à chaque fois :
multi_play(2, 2)## # A tibble: 2 × 3
## t_cost t_gain bank
## <dbl> <dbl> <dbl>
## 1 5 0 -5
## 2 5 0 -54.7. Représentation graphique d’1 joueur.
Si nous souhaitons voir l’évolution de gain d’un jour régulier participant à 20 tirages avec 10 grilles à chaque tirage :
multi_play(draw = 20, grid = 10) %>%
mutate(cumsum_cost = cumsum(t_cost), cumsum_gain = cumsum(t_gain)) %>%
rowid_to_column() %>%
pivot_longer(cols = 5:6) %>%
ggplot() +
aes(rowid, col = name, value) +
geom_line() +
geom_point() +
theme_ipsum_rc()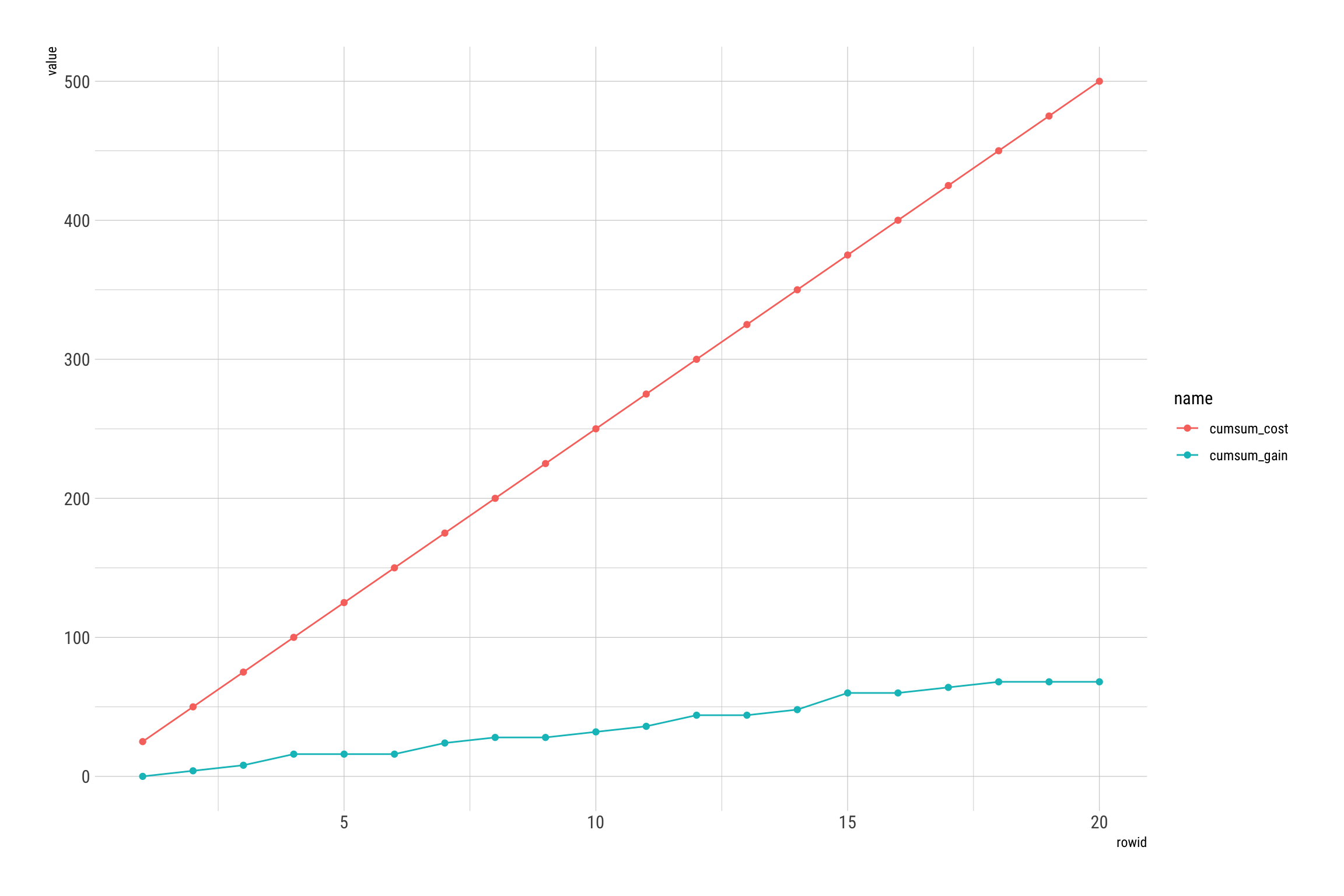
Ce joueur n’est pas très chanceux, mais peut être considéré comme un heureux gagnant à l’EuroMillions.
4.8. Appelons 20 joueurs
Pour l’expérience suivante, nous allons demander à 20 joueurs de jouer plus ou moins 1 an (100 tirages) avec le nombre de grille souhaité (un joueur peut jouer une grille et jusqu’à dix grilles).
players <-tibble(draw = rep(100, 20), grid = sample(10, 20, replace = TRUE)) %>%
rowid_to_column() %>%
mutate(game = map2(draw, grid, multi_play)) %>%
unnest(c(game)) %>%
group_by(rowid) %>%
mutate(n = 1:100) %>%
mutate(cumsum_cost = cumsum(t_cost), cumsum_gain = cumsum(t_gain)) %>%
pivot_longer(cols = 8:9)Représentation graphique :
players %>%
ggplot() +
aes(n, value, group = interaction(rowid, name), col = name) +
geom_line(size = 1) +
facet_wrap(~rowid) +
theme_ipsum_rc()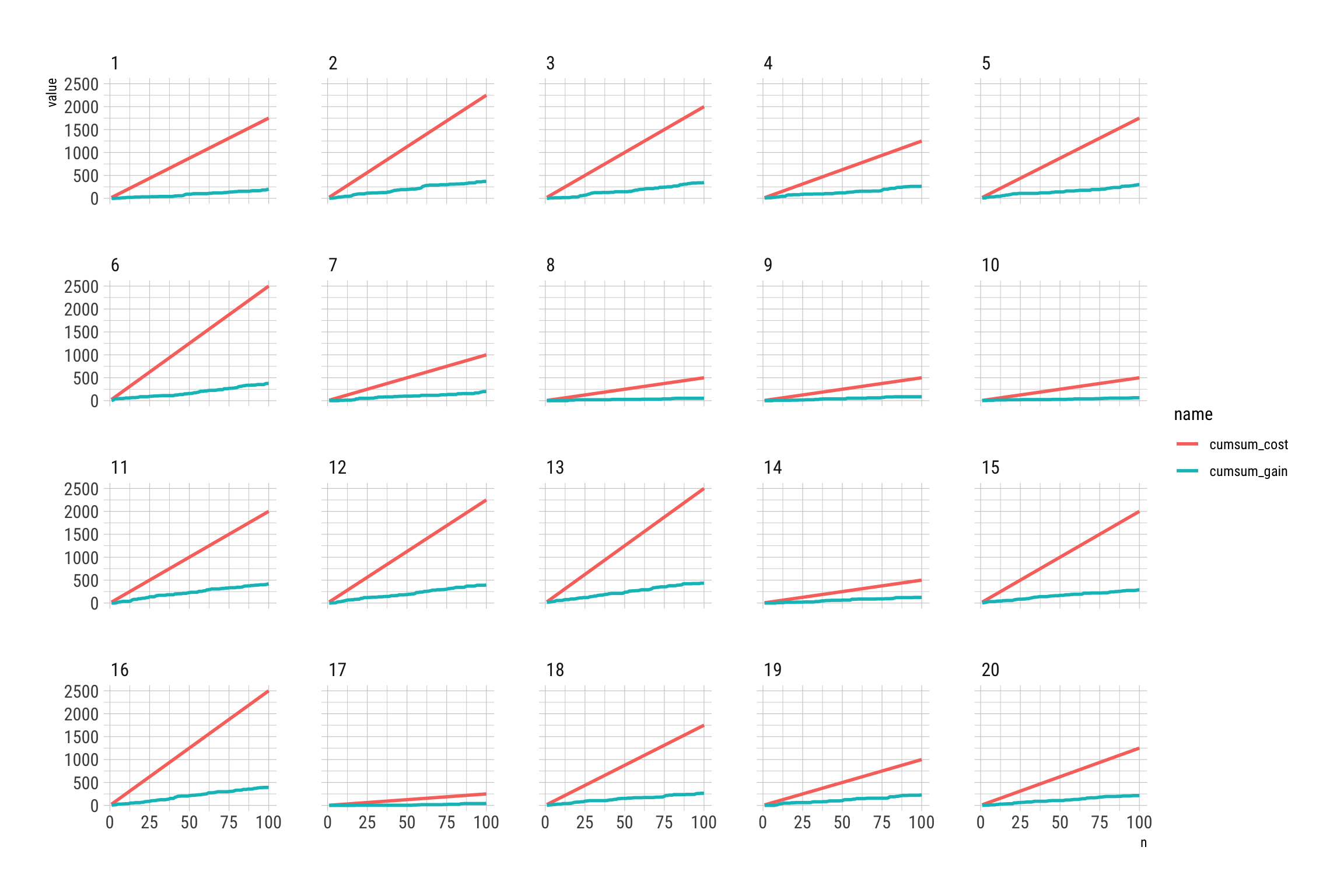
Quel joueur à le meilleur rapport gain / dépense ?
player_rank <- players %>%
group_by(rowid) %>%
summarise(cost = sum(t_cost), gain = sum(t_gain)) %>%
mutate(ratio = gain / cost, avg = 2.5 * ratio) %>%
arrange(desc(ratio))player_rank## # A tibble: 20 × 5
## rowid cost gain ratio avg
## <int> <dbl> <dbl> <dbl> <dbl>
## 1 14 1000 246 0.246 0.615
## 2 19 2000 458 0.229 0.572
## 3 4 2500 528 0.211 0.528
## 4 11 4000 838 0.210 0.524
## 5 7 2000 398 0.199 0.498
## 6 17 500 96 0.192 0.48
## 7 12 4500 792 0.176 0.44
## 8 13 5000 866 0.173 0.433
## 9 3 4000 692 0.173 0.432
## 10 9 1000 172 0.172 0.43
## 11 20 2500 428 0.171 0.428
## 12 5 3500 596 0.170 0.426
## 13 2 4500 736 0.164 0.409
## 14 16 5000 784 0.157 0.392
## 15 18 3500 528 0.151 0.377
## 16 6 5000 752 0.150 0.376
## 17 15 4000 574 0.144 0.359
## 18 10 1000 128 0.128 0.32
## 19 1 3500 404 0.115 0.289
## 20 8 1000 104 0.104 0.26Personne n’a récupéré sa mise. Le gain moyen par grille pour l’ensemble des joueurs est de :
player_rank %>%
summarise(avg_gain = mean(avg))## # A tibble: 1 × 1
## avg_gain
## <dbl>
## 1 0.429Le taux de gain pour chaque euro investi :
player_rank %>%
summarise(sum_cost = sum(cost), sum_gain = sum(gain)) %>%
mutate(rate = scales::percent(sum_gain / sum_cost)) %>%
select(rate)## # A tibble: 1 × 1
## rate
## <chr>
## 1 17%4.9. Espérance de gain
Nous pouvons calculer l’espérance de gain pour un pari. L’espérence permet de comparer des jeux de hasard dans un casino par exemple.
- Si
E > 0, il devrait participer à cet événement. - Si
E < 0, il ne devrait pas participer à cet événement.
Par contre, lorsque nous obtenons E = 0, cela signifie que l’événement est
équitable. La valeur indique le montant que nous pouvons espérer gagner en moyenne par participation. La formule est simple :
E = probabilité de gagner x montant gagné par pari – probabilité de perdre x montant perdu par pari
Calculons l’espérance de gain pour le rang 1 et le mega Jackpot de 190,000,000 € :
p <-(hyper(50, m = 5, n = 5, k = 5) * hyper(12, m = 2, n = 2, k = 2))
q <- 1-p
g <- 190000000
c <- 2.5
(p * g) - (q * c)## [1] -1.141286Nous pouvons dire qu’en moyenne nous pouvons perdre 1.14 € par grille de 2.5 € jouée en visant le jackpot. Si nous voulions l’équité pour ce jeu, le coût de la grille devrait être de 1.358714.
L’espérance de gain pour le dernier rang est de :
p <-(hyper(50, m = 5, n = 5, k = 2) * hyper(12, m = 2, n = 2, k = 0))
q <- 1-p
g <- 4
c <- 2.5
(p * g) - (q * c)## [1] -2.203187Nous voici arrivés à la fin de cet article. J’espère que cela vous a permis, tout comme à moi, de mieux comprendre le calcul de probabilité. Si vous avez aimé, partagez ou laissez un commentaire.
Bonne chance !